728x90
딥러닝 기초 - Logistic Regression Gradient Descent
시그모이드 함수
import matplotlib.pyplot as plt
import numpy as np
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))
z = np.arange(-7, 7, 0.1)
phi_z = sigmoid(z)
plt.plot(z, phi_z)
plt.axvline(0.0, color='k')
plt.ylim(-.1, 1.1)
plt.xlabel('z')
plt.ylabel('$\phi (z)$')
# y축의 눈금과 격자선
plt.yticks([0.0, 0.5, 1.0])
ax = plt.gca()
ax.yaxis.grid(True)
plt.tight_layout()
plt.show()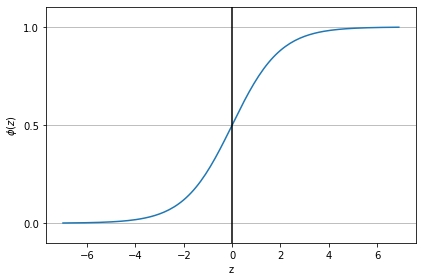
로지스틱 회귀의 비용함수 유도
def cost_1(z):
return - np.log(sigmoid(z))
def cost_0(z):
return - np.log(1 - sigmoid(z))
z = np.arange(-10, 10, 0.1)
phi_z = sigmoid(z)
c1 = [cost_1(x) for x in z]
plt.plot(phi_z, c1, label = 'J(w) y=1일 때')
c0 = [cost_0(x) for x in z]
plt.plot(phi_z, c0, linestyle='--', label = 'J(w) y=0일 때')
plt.ylim(0.0, 5.1)
plt.xlim([0, 1])
plt.xlabel('$\phi$(z)')
plt.ylabel('J(w)')
plt.legend(loc = 'best')
plt.tight_layout()
plt.show()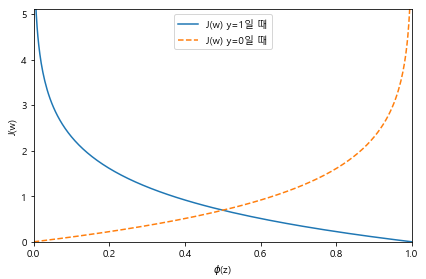
경사하강법을 이용한 로지스틱 회귀 알고리즘 구현
class LogisticRegressionGD(object):
"""
경사 하강법을 사용한 로지스틱 회귀 분류기
매개변수
------------
learning_rate : float
학습률 (0.0과 1.0 사이)
n_iter : int
훈련 데이터셋 반복 횟수
random_state : int
가중치 무작위 초기화를 위한 난수 생성기 시드
속성
------------
w_ : 1d-array
학습된 가중치
cost_ : list
에포크마다 누적된 로지스틱 비용 함수 값
"""
def __init__(self, learning_rate = 0.05, n_iter = 100, random_state=1):
self.learning_rate = learning_rate
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
"""
훈련 데이터 학습
매개변수
------------
X : {array-like}, shape = [n_samples, n_features]
n_samples개의 샘플과 n_features개의 특성으로 이루어진 훈련 데이터
y : array-like, shape = [n_samples]
타깃 값
반환값
------------
self : object
"""
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc = 0.0,
scale = 0.01,
size = 1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
net_input = self.net_input(X)
output = self.activation(net_input)
errors = (y - output)
self.w_[1:] += self.learning_rate * X.T.dot(errors)
self.w_[0] += self.learning_rate * errors.sum()
# 제곱 오차합 대신 로지스틱 비용을 계산
cost = (-y.dot(np.log(output)) - ((1-y).dot(np.log(1-output))))
self.cost_.append(cost)
return self
def net_input(self, X):
"""최종 입력 계산"""
return np.dot(X, self.w_[1:]) + self.w_[0]
def activation(self, z):
"""로지스틱 시그모이드 활성화 계산"""
return 1. / (1/ + np.exp(-np.clip(z, -250, 250)))
def predict(self, X):
"""단위 계단 함수를 사용하여 클래스 레이블을 반환"""
return np.where(self.net_input(X) >= 0.0, 1, 0)
# ≒ np.where(self.activation(self.net_input(x)) >= 0.5, 1, 0)
구현한 로지스틱 모델을 아이리스 붓꽃 이진분류 문제에 적용
# 아이리스 붓꽃 데이터 가져오기
from sklearn import datasets
import numpy as np
iris = datasets.load_iris()
X = iris.data[:, [2, 3]]
y = iris.target
print('클래스 레이블:', np.unique(y))
# 훈련 테이터와 검증 데이터 분리 및 계층화
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)
# 특성 표준화
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.transform(X_test)
# 아이리스 꽃 클래스가 0일때와 1일때만 가져와 이진분류 문제로 만들기
X_train_01_subset = X_train[(y_train == 0) | (y_train == 1)]
y_train_01_subset = y_train[(y_train == 0) | (y_train == 1)]
# 로지스틱 분류 모델로 이진 분류 작업 후 결과 확인
lrgd = LogisticRegressionGD(learning_rate = 0.05,
n_iter = 1000,
random_state = 1)
lrgd.fit(X_train_01_subset, y_train_01_subset)
plot_decision_regions(X = X_train_01_subset,
y = y_train_01_subset,
classifier = lrgd)
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc = 'upper left')
plt.tight_layout()
plt.show()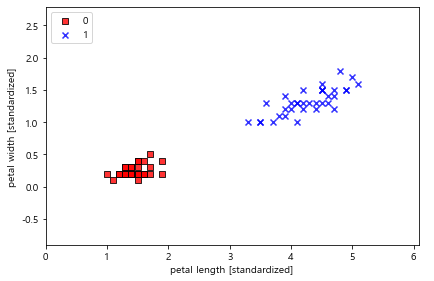
GitHub - HonorJay/diary
Contribute to HonorJay/diary development by creating an account on GitHub.
github.com
'AI' 카테고리의 다른 글
| 1209 - 의사결정나무 (0) | 2021.12.09 |
|---|---|
| 1208 - 서포트백터머신 (0) | 2021.12.08 |
| 1207 - 아달린 SGD (0) | 2021.12.07 |
| 1202 - 아달린 (0) | 2021.12.02 |
| 1201 - 퍼셉트론 (0) | 2021.12.01 |



