728x90
딥러닝 기초 - Adaptive Linear Gradient Descent
Iris 꽃 분류 문제를 해결하기위한 아달린 모델 구현
class AdalineGD(object):
"""
적응형 선형 뉴런 분류기
매개변수
------------
learning_rate : float
학습률 (0.0과 1.0 사이)
n_iter : int
훈련 데이터셋 반복 횟수
random_state : int
가중치 무작위 초기화를 위한 난수 생성기 시드
속성
-------------
w_ : 1d-array
학습된 가중치
cost_ : list
에포크마다 누적된 비용 함수의 제곱합
"""
def __init__(self, learning_rate=0.01, n_iter=50, random_state=1):
self.learning_rate = learning_rate
self.n_iter = n_iter
self.random_state = random_state
def fit(self, X, y):
"""
훈련 데이터 학습
매개변수
-----------
X : {array-like}, shape = [n_samples, n_features]
n_samples개의 샘플과 n_features개의 특성으로 이루어진 훈련 데이터
y : array-like, shape = [n_samples]
타깃 값
반환값
------------
self : object
"""
rgen = np.random.RandomState(self.random_state)
self.w_ = rgen.normal(loc = 0.0, scale = 0.01, size = 1 + X.shape[1])
self.cost_ = []
# 비용함수(Cost_Function) = 제곱오차합(SSE; Sum of Squared Errors)
for i in range(self.n_iter):
net_input = self.net_input(X)
output = self.activation(net_input)
errors = (y - output)
self.w_[1:] += self.learning_rate * X.T.dot(errors)
self.w_[0] += self.learning_rate * errors.sum()
cost = (errors**2).sum() / 2.0
self.cost_.append(cost)
return self
def net_input(self, X):
"""최종 입력 계산"""
return np.dot(X, self.w_[1:])+self.w_[0]
def activation(self, X):
"""선형 활성화 계산 ; 예제에선 항등함수를 사용하여 아무런 영향x """
return X
def predict(self, X):
"""단위 계단 함수를 사용하여 클래스 레이블을 반환"""
return np.where(self.activation(self.net_input(X)) >= 0.0, 1, -1)
- Perceptron과 다른 점

학습 및 손실값 확인
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 4))
ada1 = AdalineGD(n_iter=10, learning_rate=0.01).fit(X, y)
ax[0].plot(range(1, len(ada1.cost_) + 1), np.log10(ada1.cost_), marker='o')
ax[0].set_xlabel('Epoch')
ax[0].set_ylabel('log(Sum-squared-error)')
ax[0].set_title('Adaline = Learning rate 0.01')
ada2 = AdalineGD(n_iter=10, learning_rate=0.0001).fit(X, y)
ax[1].plot(range(1, len(ada2.cost_) + 1), ada2.cost_, marker='o')
ax[1].set_xlabel('Epoch')
ax[1].set_ylabel('log(Sum-squared-error)')
ax[1].set_title('Adaline = Learning rate 0.0001')
plt.show()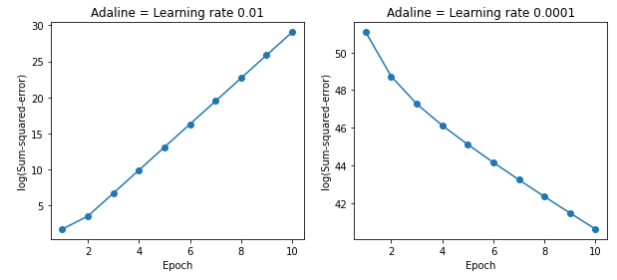
Feature Scaling - 표준화(Standardization)
평균이 0이되도록 하고 특성의 표준편차를 1(단위 분산)로 만듦.
X_std = np.copy(X)
X_std[:, 0] = (X[:,0] - X[:,0].mean())/X[:,0].std()
X_std[:, 1] = (X[:,1] - X[:,1].mean())/X[:,1].std()
표준화한 후 학습 및 그래프 확인
ada = AdalineGD(n_iter=15, learning_rate=0.01)
ada.fit(X_std, y)
plot_decision_regions(X_std, y, classifier=ada)
plt.title('Adaline - Gradient Descent')
plt.xlabel('sepal length [standardized]')
plt.ylabel('petal length [standardized]')
plt.legend(loc = 'upper left')
plt.tight_layout()
plt.show()
plt.plot(range(1, len(ada.cost_)+1), ada.cost_, marker='o')
plt.xlabel('Epoch')
plt.ylabel('Sum-squared-error')
plt.tight_layout()
plt.show()
'AI' 카테고리의 다른 글
| 1208 - 서포트백터머신 (0) | 2021.12.08 |
|---|---|
| 1207 - 로지스틱회귀 (0) | 2021.12.07 |
| 1207 - 아달린 SGD (0) | 2021.12.07 |
| 1201 - 퍼셉트론 (0) | 2021.12.01 |
| Kaggle 준비 해보기(1) (0) | 2021.08.16 |



